How to generate a finite set of points so that we can construct all of the vectors in V' is the heart of the matter. However, the first algorithm we discuss generally ignores trying to find these points. The idea is to simply generate all the possible vectors you could construct and was proposed by Monahan in 1982, though also mentioned by Sondik in 1971. To construct a vector requires selection an action and a vector in V for each observation. Thus we must generate a large number of vectors. Many of these are not useful, since they are completely dominated by other vectors over the entire belief space. We can eliminate the useless ones at the expense of some computing time, but regardless, just enumerating the vectors takes a long time even for some small problems. As a side note, it is possible to construct a problem where everyone of those vectors enumerated is useful over some portion of belief space. Thus, in the worst case, the general problem of one step of value iteration on a POMDP is very hard.
The figure below shows what the Monahan algorithm does for each action. For each observation it selects a vector from V and transforms the vectors and combines them to construct a potential vector for V'.
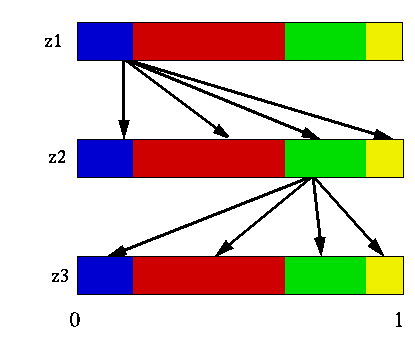
Continue
 POMDP.org
POMDP.org